Una ecuación de segundo grado o ecuación cuadrática, es una ecuación polinómica donde el mayor exponente es igual a dos. Normalmente, la expresión se refiere al caso en que sólo aparece una incógnita y que se expresa en la forma canónica:
donde a es el coeficiente cuadrático o de segundo general y es siempre distinto del número 0, b el coeficiente lineal o de primer grado y c es el término independiente.
Expresada del modo más general, una ecuación cuadrática en  es de la forma:
es de la forma:
 es de la forma:
es de la forma:con n un número natural y a distinto de cero. El caso particular de esta ecuación donde n = 2 se conoce como ecuación bicuadrática.
La ecuación cuadrática es de gran importancia en diversos campos, ya que junto con las ecuaciones lineales, permiten modelar un gran número de relaciones y leyes.
OBSERVA EL MÉTODO GRÁFICO
La ecuación completa de segundo grado tiene siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas, dadas por la fórmula general:
 ,
,
donde el símbolo "±" indica que los dos valores
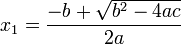
y 
son soluciones. Es interesante observar que esta fórmula tiene las seis operaciones racionales del álgebra elemental.
Si observamos el discriminante (la expresión dentro de la raíz cuadrada):
podremos saber el número y naturaleza de las soluciones:
- Dos soluciones reales y diferentes si el discriminante es positivo (la parábola cruza dos veces el eje x);
- Una solución real doble, dicho de otro modo, de multiplicidad dos, si el discriminante es cero (la parábola sólo toca en un punto al eje x);
- Dos números complejos conjugados si el discriminante es negativo (la parábola y el eje x no se cruzan).
OBSERVA EL MÉTODO FORMULA GENERAL

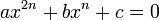

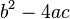
si esta informacion esta completa graciazzzzz
ResponderEliminarputo
Eliminar.l.
Pinche estupido .l. :3
Eliminark tienen mrd no ves k le estan dando pa k le ayuden idota y eso metetelo x el culo
Eliminarbuenos aportes
ResponderEliminarno entendí =(
ResponderEliminarojala puedan poner algo más explicito ;)
pues buena aportación los felicito por que esta bien graciassssssssssss por nada por que aquí la inteligente soy yoooooo jajajajajajajajajajajaja tenquiu gatetes
ResponderEliminarTas bien pendeja
Eliminar:v
Jajajaja :v
Eliminares puro choro no se crean yo no soy asi de fresa
ResponderEliminarARTPOP
ResponderEliminarno mames wey XP
EliminarQue asco de tareea b:
ResponderEliminarmarica floja
Eliminarsi no te parece pss no andes de fastioso otros queremos aprender
EliminarEste comentario ha sido eliminado por el autor.
Eliminarme kedo en las mismas gracias de todos modos
ResponderEliminartarea sarnienta del profe villa atascado marrano
ResponderEliminarno me sirvio :(
ResponderEliminarpzz medio quede igual pero gracias me sivio mucho
ResponderEliminar;)
A no pues gracias me has hecho mas dificill esto :v
ResponderEliminarpues piensa tont
Eliminarsabes pienso igual
Eliminareres mi bff
No entendi ni mierda XD
ResponderEliminarñol
ResponderEliminaryo queria ejemplos
ResponderEliminaryo queria ejemplos
ResponderEliminarno entendi ni madres
ResponderEliminarno entendi ni madres
ResponderEliminarno mames tu pendejo
ResponderEliminary del cuadrado al binomio ?
ResponderEliminara pz orale... no entendi ni madres
ResponderEliminarLa netta no
EliminarX2...
:{V
jaja sigo en las mismas
ResponderEliminaroigan nesesito ayuda con una ecuacion no se si me pueden ayudar por favor
ResponderEliminarNo es lo que busco :(
ResponderEliminarχ²+4x-8=0 queria ejemplos asi :/
ResponderEliminarBuena información,me sirvió mucho
ResponderEliminar