TEOREMA DE TALES
Si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.
Ejercicios
1.Las rectas a, b y c son paralelas. Halla la longitud de x.
2.Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?
El teorema de Thales en un triángulo
Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.
Aplicaciones del teorema de Thales
El teorema de Thales se utiliza para dividir un segmento en varias partes iguales.
Ejemplo
2. Tomando como unidad cualquier medida, se señalan en la semirrecta 3 unidades de medida a partir de A.
3. Por cada una de las divisiones de la semirrecta se trazan rectas paralelas al segmento que une B con la última división sobre la semirrecta. Los puntos obtenidos en el segmento AB determinan las 3 partes iguales en que se divide.

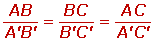










sería mejor que pusieran los problemas ya resueltos y que tuvieran una forma mas detallada de explicar las cosas
ResponderEliminarte la cabio
Eliminarsi entendi bien esta mal el ejemplo 1 no sale 5.6 sale 2.2
ResponderEliminar¿O 2.8?
Eliminarestas equivocado ...esta correcto ....es multiplicar 14 por 4 y el resultado dividirlo entre 10 y da como resultado 5.6 osea que esta resuelto correctamente
EliminarLO QUE PASÓ ES QUE LA MEDIDA DE b a c ESTÁ MAL TOMADA NO ES CUATRO ES 2 QUEDARAS 10/4 = 2/X Y SALE 2.8 SI NO ES 2 Y ES CUATRO
EliminarQUEDARÍA: 14/10 = X/4 = 5.6
Perdón la medida de b´ c´ es 2 y no 4
EliminarÉÉl proféé tiEnE la pOsTáá, es alToÓ mAmbÓó eSToo y él LoO EspLiká cHettó mÁl
Eliminarsi
ResponderEliminarhola pero como puedo encontrar ejercicios para resolver en la computadora sobre el teorema de tales
ResponderEliminarportence pillo amigo
ResponderEliminarAhre
ResponderEliminarsame bien samido
ResponderEliminarSIGAN A MATIAS PONCE EN YUTUN EL UNICO YUTUNER CON EL PENE DE BRONCE
ResponderEliminarhola alguien me puede ayudar
ResponderEliminarsi yo
Eliminarputo el que lo lea
ResponderEliminar